OPTIMIZATION OF GEOMETRY AND BUILDING ORIENTATION ON THE ACCURACY OF DISSOLVING MICRONEEDLE MASTERS USING STEREOLITHOGRAPHY

Microneedles have gained prominence as a minimally invasive transdermal drug delivery technology, offering significant advantages such as reduced pain, targeted drug delivery, and decreased medical waste. This study focuses on the optimization of dissolvable self-locking microneedles fabricated using stereolithography (SLA), with an emphasis on dimensional accuracy. Three microneedle geometries—perpendicular, concave, and convex—were investigated across three building orientations (0°, 45°, and 60°). Microneedle masters were printed using SLA and subsequently used as molds to fabricate PDMS microneedle molds. Dimensional accuracy was evaluated based on errors in height, base, and angle, with optimization conducted using the Taguchi method. The results revealed that for microneedle masters, the perpendicular geometry paired with a 45° building orientation demonstrated the best accuracy, as confirmed by S/N ratio analysis and ANOVA. For microneedle molds, perpendicular geometry remained optimal, with the 60° orientation offering reduced errors due to improved stability during the demolding process. Morphological comparisons indicated notable differences between master and mold accuracy, attributed to stresses during demolding. This study underscores the critical role of geometry and building orientation in optimizing microneedle fabrication and highlights the effectiveness of the Taguchi method in reducing dimensional errors.

1 Introduction

Microneedles have emerged as a revolutionary technology for transdermal drug delivery, offering numerous advantages over traditional methods such as hypodermic needles. Traditional drug delivery methods, such as syringes, often face challenges in effectiveness and precision. In 1970, the concept of transdermal drug delivery emerged as a way to administer drugs more effectively and with less pain by bypassing the gastrointestinal tract and liver. This approach offers several advantages, including reduced liver metabolism, more targeted drug delivery, and reduced medical waste. However, transdermal delivery faces limitations with large-molecule drugs, which led to the development of various approaches like jet injectors, iontophoresis, and microneedles. Among these methods, microneedles are considered the most effective as they penetrate the stratum corneum to deliver drugs directly to the dermis layer, bypassing the gastrointestinal tract and liver [1]. [2] [3]. Microneedles also reduce needle trauma and phobia, which is prevalent in children and up to 63% of adults, as noted in recent studies [4] [5] [6] [7] [8] [9] [10]. Microneedles are classified into four types (Fig. 1): solid, coated, dissolving, and hollow. Each has unique mechanisms for drug delivery. 

Solid microneedles create pores in the skin before drug application, coated microneedles deliver drugs by releasing drug coatings upon penetration, dissolving microneedles release their payload as the needle dissolves in the skin, and hollow microneedles transport fluids through internal channels [11] , [12]. In a study conducted by Yeung et al., hollow microneedles were fabricated using the SLA method while varying resin type, building orientation, and flow rate. This study combined hollow microneedles with a mixing chamber to mix fluorescent material. The results showed that hollow microneedles were capable of transmitting 200 µm of fluorescent material [13]. For coated microneedles, Mutlu et al. used the digital light processing (DLP) method to fabricate devices coated with gentamicin sulfate. In vitro testing demonstrated that gentamicin sulfate was released over 312 hours [14]. The solid microneedles, fabricated by Krieger et al. using the SLA method, incorporated variations in aspect ratio, needle height, and layer thickness. The study concluded that the printed microneedles had dimensions slightly lower than the theoretical ones [15]. This study focuses on dissolving microneedles due to their single-step drug delivery advantage and ease of administration [16], [17]. These microneedles typically range from 25 to 2000 µm in height, ensuring penetration without significant trauma [18]. In a study conducted by Pham et al., microneedle making was done by micro milling using CNC Micro-Milling using a flat-end mill with a diameter of 0.8 mm and using a ball-ed mill with a diameter of 0.4 mm to make a conical tip. The result has a tip diameter of less than 10 µm. This is already able to penetrate the stratum corneum. Another result is that a high feed rate can produce a shorter time but reduces the precision of the tip [19]. 

Fabrication methods for microneedles include deep-reactive ion etching, laser machining, and polymer molding using 3D printing [20] [21] [22]. Among these, 3D printing is preferred for its adaptability to diverse designs, cost-effectiveness, and rapid prototyping capabilities. Stereolithography (SLA) is particularly suitable for producing microneedles due to its ability to handle intricate designs with high resolution and aspect ratios [15]. Studies, such as those by Krieger et al. and Xenikakis et al., have demonstrated SLA’s versatility in creating microneedles with diverse shapes and dimensions [23],[24]. Building orientation significantly influences microneedle accuracy, with prior research showing varying results: orientations of 60° can enhance resolution and sharpness [25], while 45° orientations provide better structural integrity and dimensional accuracy [26]. Another study on hollow microneedles by Yeung et al. found that a 45° building orientation achieved optimal accuracy [13]. Research by Chanabodeechalermrung et al. further investigated building orientations of 0°, 15°, 45°, and 60°, showing that orientations of 15° and 45° produced the highest accuracy [27]. The geometry of microneedles also plays a critical role in ensuring mechanical stability and embedding success [28]. Three primary geometries— convex, concave, and perpendicular—have been explored in the literature. Convex designs, as proposed by Joo et al [29]., improve mechanical interlocking, while concave shapes by Choo et al. Choo et al enhance drug retention. Perpendicular geometries (sharp tipped pyramid head) by Balmert et al. simplify fabrication and ensure vertical precision [30]. Despite these advancements, there remains a lack of systematic optimization of microneedle geometry and building orientation for accurate 3D printing and subsequent molding. This study aims to address these gaps by evaluating the effects of geometry (convex, concave, and perpendicular) and building orientation (0°, 45°, 60°) on the accuracy of microneedle masters and molds fabricated via SLA. The Taguchi method is employed to systematically optimize these parameters, using signal-to-noise (S/N) ratios and ANOVA for statistical analysis.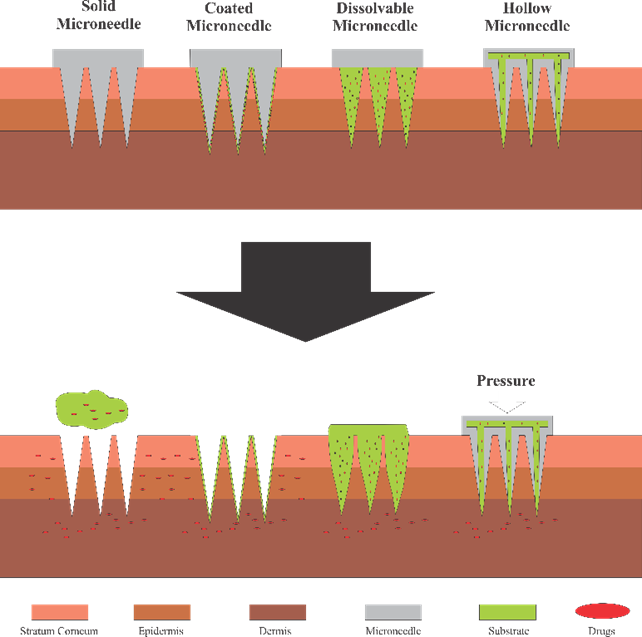

Fig. 1. Types of microneedles

2. Materials and methods

2.1 Microneedle fabrication

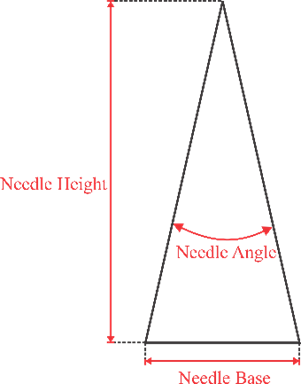
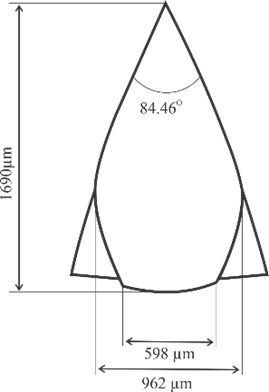
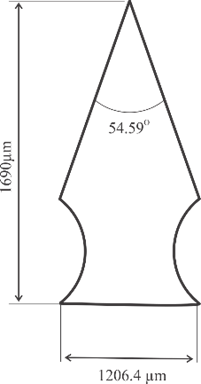
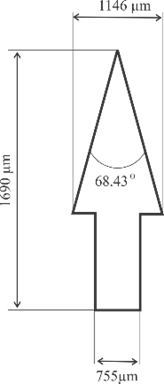
Microneedle designs were drawn using Autodesk Inventor 2021. Three geometry variations were examined, as shown in Fig. 2, including convex, concave, and perpendicular shape adopted with modifications from [25], [29], and [30] respectively. Building orientation was also examined with variations include angles of 0°, 45°, and 60°. All microneedle designs were standardized to a volume of 0.382 mm³ and a height of 1300 µm, then enlarged by 30%.

 Fig. 2. Microneedle designs of (a) general anatomy, (b) convex, (c) concave, and (d) perpendicular shape

The CAD designs, as seen in Fig. 3, were converted to G-codes and printed using Prusa SL1 stereolithography machine in a 7x7 array to form the microneedle masters. The resin material used was PLA resin (eSUN) with a viscosity of 100-270 mPa·s and a density of 1.07-1.10 g/cm3. The resulting microneedle masters were washed with isopropyl alcohol to remove residual resin. The prints were then cured at 40°C for 30 minutes using a Prusa CW 1.

Post-printing, the support structures were removed via grinding to produce flat patches. Measurements of the master microneedles, including needle base, needle angle, and needle height, were conducted using an Olympus SZX 16 Macro Microscope with LG-LSLED lighting. Measurements were taken on each side of the microneedle patch. 

Subsequently, microneedle masters served as negative molds to create microneedle molds made of polydimethylsiloxane (PDMS, Dow Corning Sylgard 184 Clear Silicone Encapsulant). The process involved (Fig. 4): 

1. Mixing PDMS with a curing agent (10:1) and stirring for five minutes. 
2. Degassing the mixture in a vacuum chamber at 0.14 MPa for 20 minutes to remove air bubbles. 
3. Pouring the degassed PDMS into a 6 cm diameter petri dish containing upright microneedles. 
4. Curing in an oven at 70°C for two hours. 

After curing, the PDMS was hardened, and the microneedles were separated from the molds. The molded microneedles underwent measurement using the same setup as the original microneedles.

Fig. 3. Example of microneedle designs in 7x7 array: (a) concave at 0°, (b) convex at 0°, (c) perpendicular at 45°, and (d) perpendicular at 60°

Fig. 4. Stages in making microneedle molding

2.2 Design of experiment

The design and optimization of dissolvable self-locking microneedles were guided by the Taguchi Method, a robust statistical tool for improving process performance and quality [31]. This method minimizes the number of experimental trials while systematically studying variable interactions using orthogonal arrays. In this study, the L9 orthogonal array was employed with two factors: geometry and building orientation, each tested at three levels. Each experimental run (see Table 1) was replicated three times to minimize the impact of random errors or variations in the fabrication process, resulting in a total of 27 specimens being tested.

Table 1. Taguchi Orthogonal Array L9

The response variable in this study was microneedle accuracy, which was assessed based on three critical dimensions: height, base, and angle. The Taguchi Method optimization used the "smaller-is-better" signal-to-noise (S/N) ratio to minimize the error rate. The S/N ratio was calculated as follows (Eq. 1).

$S/N=\ -10\ log\ \left(\ \frac{1}{n}\ \sum_{i=1}^{n}y_i^2\right)$ (1)

Where y_i^  is the response variable at a given factor level, and n is the number of responses.

Analysis of variance (ANOVA) was conducted to evaluate the statistical significance of geometry and building orientation. 

3 Result and discussion

3.1 Fabrication of microneedle master

3.1.1 Dimension accuracy

The dimensional accuracy of the fabricated microneedle masters was assessed by comparing the measured dimensions of height, base, and angle to the theoretical values shown in Fig. 2. The results, presented in Table 2, show varying degrees of error in height, base, and angle across the different building orientations and shapes. For height accuracy, the convex design exhibited the lowest error at 60° orientation (13.11%), while the concave and perpendicular designs showed higher height errors, particularly at 0° orientation. For base dimensions, errors were more pronounced, with the convex design exhibiting the highest base error at 60° orientation (63.66%), indicating challenges in replicating the outward curvature. The angle errors were generally lower across all designs, with the convex design showing the best angular accuracy at 60° orientation (9.88%).

 Fig. 5.   Microneedle measurement results on building orientation (scale bar is 1 mm). (A), (B) and (C) Perpendicular design at building orientation 0o, 45o, and 60o. (D), (E), and (F) Concave design at building orientation 0o, 45o, and 6 o. (G), (H), and (I) Convex design at building orientation 0o, 45o, and 60o

The morphology of the microneedle masters, as shown in Fig. 5, reveals distinct patterns in dimensional conformity. The perpendicular design exhibited sharp vertical profiles but was prone to base distortions at 0° orientation, which is likely due to insufficient support during printing. At 45° orientation, the perpendicular microneedles displayed better-defined features with minimal defects, while at 60° orientation, increased gravitational effects caused elongation at the base. The concave design showed the best performance at 45° orientation, with well-defined shapes and minimal dimensional distortions. However, at 0° orientation, the concave microneedles showed significant deviations from the theoretical design, particularly at the base and mid-section. At 60° orientation, irregularities near the tip were observed, indicating stability challenges during layer curing. The convex design demonstrated the most sensitivity to building orientation. At 0° orientation, the microneedles exhibited overcurved mid-sections and rounded tips, while 45° orientation produced the best overall morphology with sharper tips and smoother transitions. At 60° orientation, the convex microneedles suffered from significant base and mid-section irregularities, likely due to sagging and uneven curing.

Table 2. Measurement of 3D printed microneedle master. 

3.1.2 Taguchi optimization

The Taguchi method was utilized to identify the optimal combination of microneedle geometry and building orientation for minimizing dimensional errors. The signal-to-noise (S/N) ratio graph in Fig. 6 illustrates the influence of these factors on fabrication accuracy, based on the "smaller-is-better" criterion. 

Fig. 6. Signal to noise graph of the influence of geometry and building orientation on microneedle error accuracy

The geometry of the microneedles showed a clear influence on dimensional accuracy, with the perpendicular design achieving the highest mean S/N ratio, followed by the convex design. The concave design had the lowest mean S/N ratio, indicating higher dimensional inaccuracies. The steep slope of the geometry line in the plot highlights its significant impact on the overall error rates, which suggests that the perpendicular geometry provides the most stable and accurate microneedle fabrication among the tested designs. 

The building orientation exhibited a less pronounced effect on dimensional accuracy, as reflected in the gentler slope of the corresponding plot. Among the orientations, 0° and 45° resulted in higher S/N ratios, indicating better dimensional accuracy. However, the 60° orientation produced the lowest S/N ratio, which might be due to gravitational effects and increased mid-section distortions, particularly for geometries with curved profiles like the convex design. Based on the S/N ratio plot, the optimal combination of parameters for microneedle masters fabrication is the perpendicular geometry paired with a 45° building orientation.

3.1.3 ANOVA analysis

The results of the ANOVA analysis, as presented in Table 3, demonstrate that geometry has a statistically significant effect on microneedle mold fabrication errors, with a P-value of 0.002. Geometry also exhibits the greatest influence on error variability, as evidenced by its higher F-value and adjusted sum of squares. In contrast, building orientation shows no statistically significant effect, as indicated by a P value of 0.322 and a lower F-value. While the signal to-noise analysis highlighted its impact, particularly at orientations like 45° and 60°, the ANOVA results suggest that its role is secondary compared to geometry.

Table 3. ANOVA results for the effects of geometry and building orientation on error of microneedle.

3.2 Fabrication of microneedle molds

3.2.1 Dimensional accuracy

The error rates for the dimensions of the fabricated microneedle molds are shown in Table 4. The perpendicular design consistently demonstrated the lowest height errors, with the smallest value observed at 60° orientation. In contrast, the concave design showed the highest height error, particularly at 0° orientation, likely due to the challenges in maintaining its inward curvature during the PDMS molding process. The convex design exhibited moderate height errors, with the best performance at 60° orientation. For angle errors, the perpendicular design displayed the lowest angle errors across all orientations, with the best accuracy observed at 60° orientation. The convex design demonstrated a wider range of angle errors, with the lowest value at 45° orientation. The concave design, however, exhibited the largest angle errors, with the highest value recorded at 0° orientation.

Table 4. Measurement of microneedle molds

The morphology of the microneedle molds is shown in Fig. 7. In general, the printed microneedles master and molds exhibit similar dimensional trends, although minor deviations are observed. These deviations can be attributed to the demolding process, where deflection occurs due to the pulling forces exerted on the PDMS during separation from the microneedle master. This pulling effect introduces small distortions, particularly in dimensions such as the base and angle, leading to slight differences between the molded microneedles and their masters. At higher building orientations, the geometry of the microneedle sides often results in additional material deposition or support structures. This additional material enhances the structural integrity of the printed microneedle, making the molding release process smoother and reducing the likelihood of damage to the mold. Consequently, errors in the molded microneedles are minimized at steeper orientations, as the improved stability of the master reduces distortion during the separation phase.

 Fig. 7. Microneedle molding measurement results on building orientation (scale bar is 1 mm). (A), (B) and (C) Perpendicular design at building orientation 0o, 45o, and 60°. (D), (E), and (F) Concave design at building orientation 0°, 45°, and 60°. (G), (H), and (I) Convex design at building orientation 0°, 45°, and 60°

3.2.2 Taguchi optimization

The signal-to-noise (S/N) ratio plots shown in Fig. 8 illustrate the performance of geometry and building orientations on molding error. 

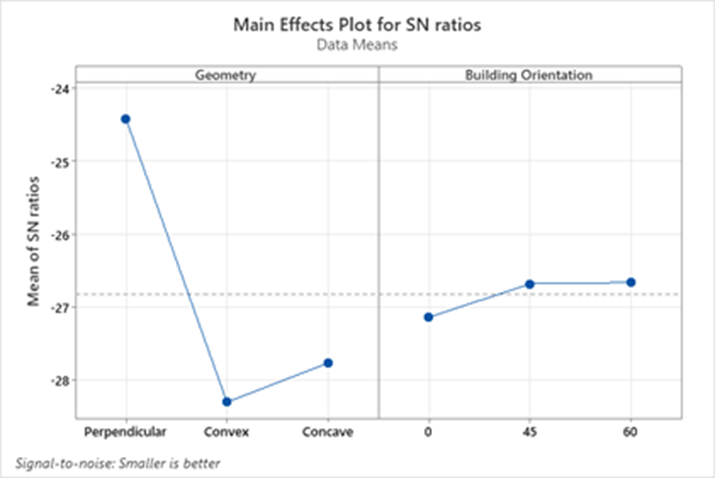
Fig. 8. Signal to noise graph of the influence of geometry and building orientation on error rate of microneedle molds

The geometry factor had a significant impact on dimensional accuracy, as indicated by the steep slope of the geometry plot. The perpendicular geometry displayed the highest mean S/N ratio, reflecting the lowest overall error rate and the best dimensional accuracy. This was followed by the convex geometry, while the concave geometry showed the lowest S/N ratio, corresponding to the highest error rates. The building orientation also influenced dimensional accuracy, though less significantly than geometry, as suggested by the gentler slope in its plot. Among the tested orientations, 45° and 60° orientations yielded comparable S/N ratios, indicating similar accuracy levels. However, the 0° orientation showed a much lower S/N ratio, indicating substantially higher dimensional deviations.

3.2.3 ANOVA analysis

The results of the ANOVA analysis, as presented in Table 5, demonstrate that geometry has a statistically significant effect on microneedle mold fabrication errors, with a P-value of 0.002. Geometry also exhibits the greatest influence on error variability, as evidenced by its higher F-value and adjusted sum of squares. In contrast, building orientation shows no statistically significant effect, as indicated by a P value of 0.322 and a lower F-value. While the signal to-noise analysis highlighted its impact, particularly at orientations like 45° and 60°, the ANOVA results suggest that its role is secondary compared to geometry.

3.3 Discussion

The morphological comparison between microneedle masters and molds reveals notable differences in accuracy and dimensional conformity across the tested geometries and building orientations. For the perpendicular design, the masters exhibit smooth and uniform features across all orientations, with consistent height and angle compared to other geometries. These results align with previous studies that demonstrate the advantage of simpler, vertical geometries in reducing dimensional errors during stereolithography (SLA) printing, as such designs allow for uniform resin deposition and minimal distortions during curing [30]. However, the molds show slight distortions, particularly at 0°, where base accuracy is compromised due to stress during demolding. At 45° and 60°, the molds better conform to the master designs, likely due to improved resin flow and reduced gravitational effects during printing [25]. Previous studies have found that angled orientations enhance structural stability during SLA fabrication [32]. In contrast, the concave design struggles to maintain its inward curvature, particularly at 0°, where height and angle are less defined. These findings are consistent with research by Choo et al., which highlights the challenges in printing geometries with inward curvatures due to uneven layer stacking and increased susceptibility to resin shrinkage during curing [25]. The molds of the concave geometry show even greater distortions, with wider bases and less sharp tips. This can be attributed to additional stresses during demolding, which exacerbate inaccuracies in complex designs [33]. Meanwhile, the convex design exhibits moderate conformity in both masters and molds. At 0° and 45°, the convex geometry produces smoother results compared to the concave design but still displays slight base distortions in the molds. The 60° orientation performs best, achieving the best accuracy in both masters and molds, which is likely due to the enhanced structural rigidity provided by outward curvatures during both the printing and demolding processes [29]. Base distortion causes morphological forms that are less in accordance with the design, especially in building orientations of 45o and 60o. This is because the building orientations of 45o and 60o show separate parts during the printing process, this happens because there is no support. In the convex design, base distortion is not very visible because the design is equipped with thin support. This can be seen in Fig. 9 – 11. 

Tabel 5. ANOVA results for the effects of geometry and building orientation on error of microneedle molds

Fig. 9. Printing process on concave design

Fig. 10. Printing process on perpendicular design

Fig. 11. Printing process on convex design

The Taguchi optimization results indicate that the best performance for microneedle masters is achieved with the perpendicular geometry at a 45° building orientation. Both geometry and building orientation significantly influence the dimensional accuracy of the masters, as demonstrated by the results of ANOVA. The perpendicular geometry benefits from its simple and uniform structure, which minimizes gravitational and resin-flow-related distortions during SLA fabrication [13]. The 45° orientation balances resin deposition and reduces gravitational effects, making it particularly effective for achieving dimensional accuracy in the masters [13]. For microneedle molds, the optimal combination is perpendicular geometry at either 60° or 45° orientation, with geometry being the only statistically significant factor. The perpendicular geometry ensures uniform resin deposition and easier demolding, leading to better replication accuracy, as also highlighted in similar molding studies [30]. The observed difference in the optimal orientation between masters and molds can be attributed to the additional stresses introduced during the demolding process. At 60°, the added material stability reduces stress during separation from the mold, resulting in fewer dimensional distortions. These findings align with Choo et al.’s conclusions on the role of higher orientations in improving post fabrication stability [25]. While 45° also performs well, its effectiveness is slightly less due to the balance between resin deposition and support stability, as demonstrated in prior SLA optimization studies [26], [27], [32]. 

4 Conclusions

This study explored the effects of geometry and building orientation on the dimensional accuracy of dissolvable microneedles fabricated using stereolithography. Three geometries—perpendicular, concave, and convex—were evaluated across building orientations of 0°, 45°, and 60° to optimize the fabrication of microneedle masters and molds. The Taguchi method and ANOVA analysis were employed to identify optimal parameters and their significance. The results demonstrated that the perpendicular geometry exhibited superior accuracy across all fabrication stages. For microneedle masters, the combination of perpendicular geometry and a 45° building orientation provided the lowest dimensional errors, benefiting from uniform resin deposition and balanced structural stability. For microneedle molds, the perpendicular geometry paired with a 60° orientation achieved the best performance due to reduced demolding stresses and improved material stability. Morphological analysis revealed differences between microneedle masters and molds, with molds showing slight distortions attributed to demolding forces. Building orientation significantly impacted fabrication accuracy, with steeper angles enhancing structural stability but increasing mid-section distortions in more complex geometries like concave and convex designs. These findings highlight the critical role of geometry and building orientation in optimizing microneedle fabrication and demonstrate the effectiveness of the Taguchi method for systematic optimization.

This research was funded by the Universitas Gadjah Mada Final Project Recognition Program Grant for Fiscal Year 2024 (RTA 2024) based on assignment letter number 5286/UN1.P1/PT.01.03/2024.

The authors declare that there is no conflict of interest regarding the publication of this article.

Christoforus Yacob Sianipar: Conceptualization, methodology, formal analysis, validation, investigation, visualization, writing – original draft; Indriani Yosida Erline: Investigation, formal analysis, methodology, writing – original draft; Wangi P. Sari: Conceptualization, formal analysis, resources, supervision, funding acquisition, writing – review & editing.

There is no associated dataset available for this study.

No supplementary materials are included in this manuscript.